Methodology¶
Below we describe the methods implemented by kPAL.
k-mer counting¶
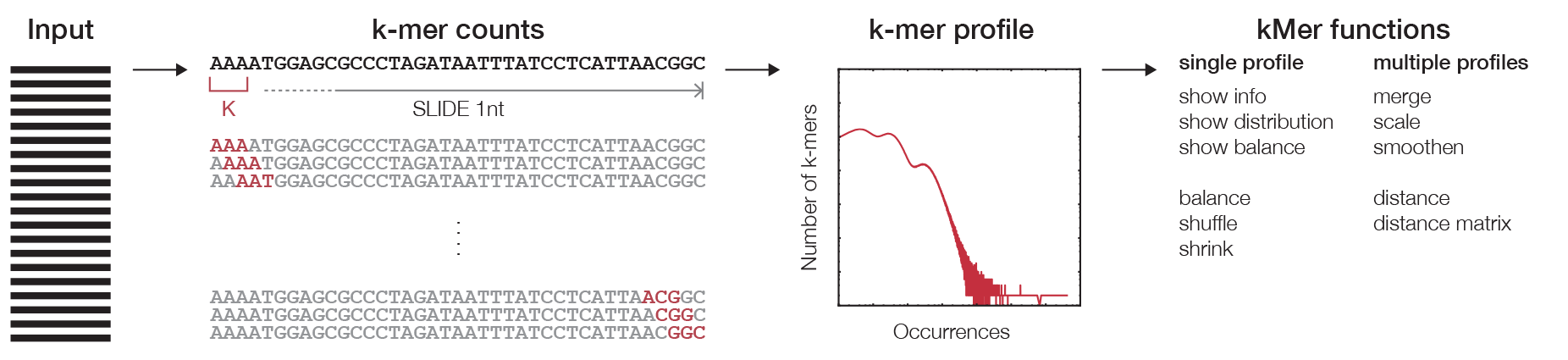
The first step in any k-mer analysis is the generation of a profile (Figure 1), which is constructed by the counting algorithm. The efficiency of the algorithm is improved by encoding the DNA string in binary following this map:
| Base | Binary |
|---|---|
| A | 00 |
| C | 01 |
| G | 10 |
| T | 11 |
Subsequently, the binary encoded k-mers are used as the index of a count table. This can be achieved by the concatenation of the binary code for each nucleotide in a given DNA string. This procedure eliminates the need to store the actual k-mer sequences since they can be retrieved from decoding the offset in the count table. The binary code for each nucleotide is chosen in such a way that the complement of the nucleotide can be calculated using the binary NOT operator. The counting algorithm returns a profile that holds observed counts for all possible substrings of length k that can be stored for other analyses.
Distance metrics¶
Since the k-mer profile is in essence a vector of almost independent values, we can use any metric defined for vectors to calculate the distance between two profiles. We have implemented two metrics which are the standard Euclidian distance measure and the multiset distance measure (1). The last metric is parameterised by a function that reflects the distance between a pair. We have implemented two pairwise distance functions (2) and (3).
For a multiset \(X\), let \(S(X)\) denote its underlying set. For multisets \(X, Y\) with \(S(X), S(Y) \subseteq \{1, 2, \ldots, n\}\) we define:
Strand balance¶
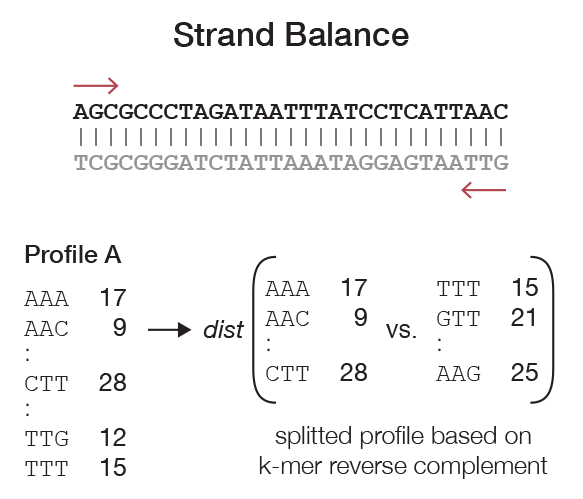
When analysing sequencing data, which frequently consist of reads from both strands (e.g., due to non strand-specific sample preparation or paired-end sequencing), we can assume that the chance of observing a fragment originating from the plus and minus strands are equal. Additionally, if the sequencing depth is high enough, we expect a balance between the frequencies of k-mers and their reverse complement in a given k-mer profile. Every type of NGS data has an expected balance (i.e., SAGE is not expected to yield a balanced profile while whole genome shotgun sequencing is expected to have a perfectly balanced frequency between k-mers and their reverse complement). Thus, k-mer balance can indicate the quality of NGS data in respect to over-amplification, insufficient number of reads, or poor capture performance in the case of whole exome sequencing.
To calculate the balance, first we observe that every k-mer has a reverse complement. One of these is lexicographically smaller (or equal in the case of a palindrome) than the other. We first split a profile into two vectors, \(A = (a_0, a_1, \ldots)\) and \(B = (b_0, b_1, \ldots)\) and where \(b_i\) represents the reverse complement of \(a_i\) and vice versa. The distance between these vectors can be calculated in the same way as described for pairwise comparison of two full k-mer profiles (Figure 2).
Additionally, kPAL can forcefully balance the k-mer profiles (if desired) by adding the values of each k-mer to its reverse complement. This procedure can improve distance calculation if the sequencing depth is too low.
Profile shrinking¶
A profile for a certain k-mer length contains information about k-mers of smaller lengths. This can be seen from the fact that a word \(w\) over an alphabet \(\mathcal{A}\) has \(|\mathcal{A}|\) possible suffixes of length one. To calculate the number of occurrences of \(w\), we simply need to calculate \(\sum_{i \in \mathcal{A}} count(w.i)\). This only holds when the k-mer length is relatively small compared to the length of the original sequences. Indeed, if a sequence of length \(l\) is used for counting at length \(k\), then \((l - k + 1)\) k-mers are encountered per sequence. However, shrinking of a profile will yield \((l - k)\) k-mers. Usually, this border effect is small enough to ignore, but should be taken into consideration when counting in large amounts of small (approaching length \(k\)) sequences. Shrinking is useful when trying to estimate the best \(k\) for a particular purpose. One can start with choosing a relatively large \(k\) and then reuse the generated profile to construct a profile of smaller \(k\) sizes (Figure 3).
Scaling and smoothing¶
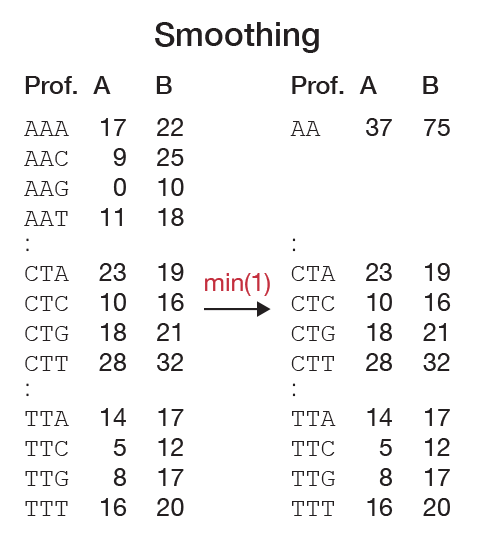
Ideally, the samples that are used to generate profiles are sequenced with the same sample preparation, on the same platform, and most importantly at sufficient depth. However, in practice, this is rarely the case. When two similar samples are sequenced at insufficient depth, it will be reflected in a k-mer profile by zero counts for k-mers that are not expected to be nullomers. While this is not a problem in itself, the fact that most sequencing procedures have a random selection of sequencing fragments will result in a random distribution of these zero counts. When comparing two profiles, the pairwise distances will be artificially large. Scaling the profiles can partially compensate for differences in the sequencing depth but cannot account for nullomers since no distinction can be made between true missing words and artificially missing words. An obvious solution would be to shrink the profile until nullomers are removed. This method is valid as long as all zero counts reflect artificial nullomers. Otherwise, shrinking will reduce the specificity and does not reflect the true complexity of the sequenced genome. To deal with this problem, we have developed the pairwise smoothing function. This method locally shrinks a profile only whe necessary. In this way, we retain information if it is available in both profiles and discard missing data (Figure 4).
Let \(P\) and \(Q\) be sub-profiles of words over an alphabet \(\mathcal{A}\) of length \(l\) (with \(l\) devidable by \(|\mathcal{A}|\)). Let \(t\) be a user-defined threshold and let \(f\) be a method of summarizing a profile. If \(min(f(P), f(Q)) > t\) we divide the profiles in \(|\mathcal{A}|\) equal parts and recursively repeat the procedure for each part. If this is not the case, we collapse both \(P\) and \(Q\) to one word. Implemented methods of summarizing are minimum, mean, and median. In Figure 4 we show an example of how smoothing might work. We have chosen \(f = min\) and \(t = 0\) as default parameters.With this method, we can count with a large k-mer length \(k\) and retain the overall specificity of the profile since this method can automatically select the optimal choice of \(k\) locally.